네거티브 피드백 증폭 회로
네거티브 피드백(부귀환)
입력과 출력의 관계를 정하는 것이 있을 때 출력의 일부가 입력에 반영되는 것을 '귀환(Feed back)'이라고 합니다. 여기서 출력의 증가(혹은 감소)가 입력에 반영되었을 때, 귀환한 시그널이 입력과 같은 증감을 나타내는 귀환을 '정귀환'이라고 합니다.
예를 들어, 교실 선생님이 마이크를 통해 말하는 목소리의 크기를 학생이 '크다'라고 전했을 때, 선생님이 마이크 음량을 더욱 크게 하는 장면은 정귀환이라고 할 수 있을 것입니다. 또 반대로 선생님이 마이크를 통해 말하는 목소리의 크기를 학생이 '작다'라고 전했을 때 선생님이 마이크 음량을 더 줄이는 장면도 정귀환이라고 할 수 있습니다. 이처럼 정귀환에서는 약간의 변화가 귀환에 의해 강화되기 때문에 극단적인 결과에 이른다는 특징이 있습니다.
한편, 출력의 증가(혹은 감소)가 입력에 반영되었을 때, 귀환한 시그널이 입력과 반대의 증감을 나타내는 귀환을 '음귀환'이라고 합니다. 예를 들면, 교실의 선생님이 마이크를 통해서 말하는 소리의 크기를 학생이 '크다(작다)'라고 반환했을 때, 선생님이 마이크 음량을 작게(크게) 하는 경우입니다. 이때는 귀환에 의해 변화가 억제되기 때문에 전체가 안정화되는 특징이 있습니다.
네거티브 피드백 신호 흐름
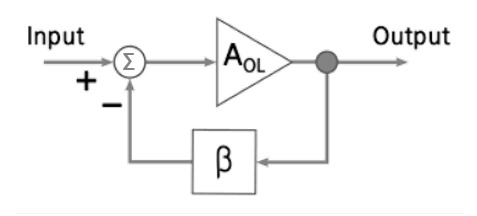
먼저 전체에 대한 입력은 X로 표현되며 출력은 Y라고 적혀있습니다. 그리고 A로 적힌 상자로 표시되는 요소는 입력된 신호의 A 배를 출력함으로써 입력 신호를 증폭합니다. 이 A는 '개루프 증폭률(Open-loop gain)'이라고 불리며 귀환하지 않을 때의 증폭률을 나타냅니다.
β라고 적힌 상자로 표시되는 요소는 이 요소의 입력한 신호의 β 배를 출력함으로써 출력 Y의 일부를 입력 측으로 귀환하는 기능을 가집니다. 이 β는 '귀환율(Feedback transfer function)'이라고 불리며 출력이 입력에 반영되는 정도를 나타냅니다.
마지막으로 Σ 기호로 쓰인 둥근 요소는 + 입력에서 − 입력을 뺀 것을 출력하기 때문에 두 신호의 차이를 잡는 역할을 합니다. 또한 A, β의 곱은 '루프 이득(Loop gain)'이라고 불리며 루프를 한 바퀴 돌고 다시 돌아왔을 때의 배율을 나타냅니다. 또 1+βA는 '귀환량'이라고 불립니다. 그리고 네거티브 피드백 시스템 전체의 증폭률 G는 '폐루프 증폭률(Closed-loop gain)'이라고 불리며 G= Y/X = A/(1 + βA)로 표현됩니다.

장점1. 전체 증폭률이 변동되기 어렵습니다.
A라고 적힌 상자는 플러스 입력 단자와 마이너스 입력 단자의 전압 차이를 A 배로 증폭하여 출력하는 것으로 '차동 증폭 회로'라고 불립니다. 이 회로에서는 출력 전압이 저항 R1 그리고 R2에 의해 분할된 것이 마이너스 입력 단자로 되돌아갔기 때문에 피드백률이 β=R1/(R1+R2)의 부귀환이 발생하고 있습니다. 따라서 이 회로 전체의 증폭률은 G=A/(1+βA)입니다.
이 증폭률 G는 A가 무한대로 가정하면 G=1/β=1+R2/R1와 같이 근삿값으로 표현할 수 있습니다. 즉 회로 고유의 값인 A가 제조 편차나 온도 변화 등으로 변동해도 A가 어느 정도 큰 값이기만 하면 그 값 자체는 회로 전체의 증폭률에 나타나기 어렵다고 할 수 있습니다. 이와 같이 음귀환을 곱함으로써 회로 고유의 파라미터가 회로 전체의 성능에 미치는 영향을 약화시킴으로써 보다 안정적인 회로 성능을 실현할 수 있습니다.

장점2. 주파수 특성 개선이 가능합니다.
일반적으로 증폭 회로의 증폭률 A는 입력하는 신호의 주파수가 커지면 저하되고, 대략적으로 근사하면
A(f)=A0/1+j(f/fc) 와 같이 변합니다.(단 j는 허수 단위) 이 주파수 의존성을 양 대수 플롯에서 컷오프 주파수 fc를 초과하면 증폭률이 저하됩니다. 이러한 증폭회로를 사용해서 입력신호의 파형을 바꾸지 않고 진폭만을 증폭하기 위해서는 취급하는 신호가 포함하는 스펙트럼의 상한 주파수보다 fc가 큰 증폭 회로가 되어야 합니다.
네거티브 피드백을 곱함으로써 효과적인 컷오프 주파수가 (1+βA0) 배로 확대하고 있고, 그만큼 넓은 주파수대에서 일정한 증폭률을 보인 것을 알 수 있습니다. 이와 같이 네거티브 피드백을 곱함으로써 증폭률이 일정한 주파수 범위를 확대하고 회로 전체로서의 주파수 특성이 개선됩니다.
장점3. 입출력 임피던스를 변경할 수 있습니다.
차동 증폭 회로를 입력 임피던스 Zin, 출력 임피이던스 Zout를 포함하여 소신호 등가 회로로 표현합니다. 저항 R1, R2에 의해 출력 전압을 저항 분할하여 네거티브 피드백을 걸면 회로 전체로서의 입력 임피던스는 (1+βA) 배가되고, 또한 출력 임피던스는 1/(1+βA) 배가 되는 것을 계산에 의해 도출할 수 있습니다.
전압을 읽고 전압을 출력하는 증폭 회로에서는 입력 임피던스가 높고 출력 임피던스가 낮은 쪽이 좋기 때문에 음귀환을 곱함으로써 두 성능 모두 개선했다는 것이 됩니다. 이 밖에도 전압 입력&전류 출력, 전류 입력&전압 출력, 전류 입력&전류 출력 등의 신호 조합을 생각할 수 있는데, 어떤 경우라도 음귀환에 의해 입출력의 임피던스를 변화시킬 수 있습니다.
장점4. 비선형 성을 억제 할 수 있습니다.
이상적인 신호 증폭 회로에서는 작은 진폭의 입력 신호 x 및 출력 신호 Y의 사이에는 Y=Ax라고 하는 선형적인 관계가 성립됩니다. 그렇지만 현실에서는 사용하는 신호의 진폭의 범위 내에서 엄밀하게 직선이라고는 말할 수 없고, 다소라도 곡선 형태를 가지지만 신호 증폭 회로의 비선형성이라고 합니다.
이러한 비선형성으로 증폭기의 입출력 특성은 x에 정현파가 입력했을 때의 출력 신호에는 고조파 성분이 생겨, 실제의 신호 파형을 왜곡시킵니다. 이때의 변형 정도는 '고조파 왜곡(Total harmonic distortion): THD'에 의해 평가할 수 있습니다. 그런데 여기에 네거티브 피드백을 걸면 증폭기가 본래 가지는 비선형성을 대폭 억제할 수 있습니다. 이와 같이 네거티브 피드백에 의해 비선형성이 억제되어 회로 전체적으로 보다 선형성이 높은 것을 얻을 수 있습니다.
'디지털 전자회로' 카테고리의 다른 글
| 조합 논리회로 (0) | 2024.02.16 |
|---|---|
| 디지털 회로의 논리 회로 (0) | 2024.02.15 |
| 연산 증폭기 응용 (1) | 2024.02.09 |
| 연산 증폭기 (1) | 2024.02.08 |
| 증폭 회로의 주파수 특성 개선 방법 (0) | 2024.01.30 |
| 트랜지스터의 주파수 특성 (1) | 2024.01.29 |
| 트랜지스터 데이터 시트 확인 사항 (2) | 2024.01.27 |
| 포토트랜지스터 (1) | 2024.01.26 |


댓글